— 试用于COVID-19疫情分析和预测
章其初博士 2020年2月17日
摘要:本研究工作建立的传染病动力学SARD新型模型,迈出模型计算的一大步,从疫情函数没有解析解到有解析解。利用本模型,计算得到湖北外地区COVID-19流行病疫情数据与通报数符合非常好。因而模型能定量给出传染病疫情几个月全过程的全部病例统计量,误差小且可靠。
1、传染病动力学SARD新型模型
2019年12月新型冠状病毒2019-nCoV引起的新冠肺炎(后由世界卫生组织命名为COVID-19)流行病爆发以来,中国和其他国家很多研究机构和高等院校的流行病、统计学及其他专业学者进行了大量建模计算,进行疫情分析和预测。
传染病建模计算早在20世纪初就开始了,1927年Kermack与McKendrick在研究流行于伦敦的黑死病时提出的SIR舱室模型,是传染病模型中最经典、最基本的模型,为传染病动力学的研究做出了奠基性的贡献。模型中把传染病流行范围内的人群分成三类:S类为易感者(Susceptible),指未得病者,但缺乏免疫能力,与感病者接触后容易受到感染;I类为感病者(Infective),它可以传染给S类成员;R类为移出者(Removal),指被隔离,或因病愈而具有免疫力的人。在若干假设下,模型导出S、I、R三个函数的一阶微分方程组。方程组函数三个S、I、R没有解析解。疫情预测只能根据已有数据得到的拟合曲线,并外延用来预测。因而只能对疫情进行定性预测,给出定量预测值困难,或偏差大。随后,很多传染病学者提出了其他很多模型,甚至更复杂模型,尝试建模计算数据与病例统计数据拟合更接近。
本研究工作的目标是寻找疫情关键函数的解析解。参考前人的模型,本文作者反复思考和在计算机上定量计算试验,提出传染病动力学SARD新型模型,并提出痊愈率是逻辑回归函数,一个大胆但合理的假设。模型中4个函数,S、A、R、D有解析解。并用于COVID-19疫情定量分析和预测。
SARD模型中4个函数,S、A、R、D,分别称为易感者,累计感病者,累计痊愈者,累计死亡者。现有感病者函数I不包括在模型方程内。
SARD模型中痊愈率和死亡率定义如下:
-
累计痊愈者R等于痊愈率乘A。
-
累计死亡者D等于死亡率乘A。
模型中每日新增感病B等于当日累计感病者A数减去昨天的,现有感病者I等于A减去R,再减去D。
这里SARD模型中的痊愈率与SIR模型中定义不同。
在若干假设下,推导得到SARD模型中的四个函数S、A、R、D的一阶微分方程组。
求解A的一阶微分方程,得到了累计感病者函数A的解析解,是逻辑回归函数。
另外,本模型提出一个大胆但合理的假设,痊愈率也是逻辑回归函数。
死亡率可以采用疫情数据的线性函数拟合,得到死亡率函数的两个参数。线性函数一次方系数等于零,对应为死亡率采用疫情数据平均值。
这样,采用SARD模型,选取传染病疫情5~11天的累计感染者A、痊愈者R和死亡者D的数据,在传染病疫情期间的关键数据全部可以计算得到,并可进行定量疫情预测,给出累计感染者A、新增感染者B、痊愈者R、死亡者D以及现有感病者I每天数量。
采用SARD模型计算也可计算得到疫情的其他参数。如基本传染数Ro,只要知道传染者传染周期(天数),就可计算得到。即上述选用疫情期间的少量可靠天数数据,通过SARD模型计算,就可计算得到早期的Ro,预测Ro小于1的日期等。从已经发表的论文中看出,选用疫情早期通报数据,计算得到的Ro往往偏差大。另外不同学者分析相同疫情得到的Ro也一致性差。这是由于疫情早期数量小,统计学上涨落大,以及收集汇总数据误差大。
有关流行病学者和公众关心的拐点问题说明如下。流行病统计学通常把现有确诊人数最大日作为拐点。现有确诊人数在最大日期的前后一天,差别比较小,另外流行病统计数量也有一定偏差,所以这里把现有感病者数I最大日的前后共3天作为现有感病者数最大日期区,对应拐点区。另外,传染病统计学习惯称为拐点与数学定义不同,数学中函数的拐点是函数二阶导数为零的点。
2、传染病SARD模型计算COVID-19疫情主要结果
利用SARD模型,计算得到COVID-19流行病疫情主要数据与通报数接近,表明模型适用于这类流行病的分析。因而定量预测疫情发展趋势数比较可靠。
传染病SARD模型计算预测COVID-19疫情,全国累计感染总数 7万8千人,相对偏差3%。
湖北外其他地区疫情
建模计算采用2月4~14日(11天)数据。
-
预测累计感染者总数1万3千人,相对偏差3%。
-
在1月24~26日的三天内Ro平均值2.8,误差±0.3。
在2月6到7日期间,Ro小于0,日期偏差1天。
传染周期选用12天。
-
预测现有确诊人数拐点区在2月9到11日,与中国卫生健康委员会通报的日期相同。预测最大确诊人数9千4百人,相对偏差3%。
-
疫情预期在3月6日到7日期间走向尾声,那时现有确诊人数小于5百人。
很多地级市现有确诊人数将清零。
-
疫情末期痊愈率达98.6%左右。
-
预测死亡人数140人左右。
湖北地区疫情
建模计算采用2月13~17日(5天)数据。2月5日到12日的8天,计算数值与通报数值偏差大,可能通报数据不可靠。
-
预测累计感染者总数6万5千人,相对偏差3%。
-
在1月24~26日的三天内Ro平均值3.6,误差±0.3。
在2月12到13日期间,Ro小于1,日期偏差1天。
传染周期选用12天。
-
预测现有确诊人数拐点区在2月17到19日区,最大人数5万人,偏差3%。
-
疫情在3月23日到24日走向尾声,那时现有确诊人数小于5百人。
-
疫情末期痊愈率达96.3%左右。
-
预测死亡人数2300人左右。
3、建模计算COVID-19疫情的详情及分析和讨论
传染病COVID-19疫情的SARD模型计算要点如下。
模型中各类名称A、R、D和I与中国卫生健康委员会报告中的病例名称有一一对应关系。累计感病者A数对应累计确诊病例数,累计新增感病者B数对应新增确诊病例数,累计痊愈者R数对应累计痊愈病例数,累计死亡者R数对应累计死亡病例数,现有感病者A数对应现有确诊确诊病例数。
模型计算时,首先,选用合适的通报数据用于模型拟合,通常选用最近5到11天的数据。选用的数据要比较可靠,因为统计病例过程是比较复杂,容易出错。这里COVID-19疫情数据,采用网上查找得到的数据,可能与中国卫生健康委员会报告原始数据有一些偏差。
湖北地区建模计算采用2月13~17日(5天)数据,因为12日和13日通报数据一天差1万4千多人。认为12日及其前几天数据不可靠。
模拟拟合累计感病者A的逻辑回归函数,得到函数A的两个参数,分别对应累计感病者总数N和所谓接触概率与感染概率的乘积。模拟拟合痊愈率的逻辑回归函数,得到函数痊愈率的两个参数。
建模计算分别处理湖北外其他地区和湖北地区两部分COVID-19流行病疫情。通报病例数和建模计算得到的数据在下面十个图中给出。图中离散点是疫情通报的数值,实线是SARD模型计算的数据。
湖北外其他地区,通报病例数和建模计算得到的数据,在图1-5中给出。从图1看出,累计确诊数A模型计算数据与通报数,除了刚开始几天外,在相当宽日期范围内符合良好。图2中新增确诊数B计算数据与通报数据偏离较大,这是由于B是累计确诊A的相邻一天差,数值比较小。并且,根据误差理论,B的偏差是A的两倍。但无论如何,通报数据基本还是分布在计算数据曲线的两侧。图3中现有确诊数I模型计算与通报数符合良好,拐点区一致,在2月9-11日期间。图4和图5中痊愈率和累计痊愈病例数R模型计算与通报数据相当一致,说明本文大胆提出的第二条假设,痊愈率也是逻辑回归函数非常合理。
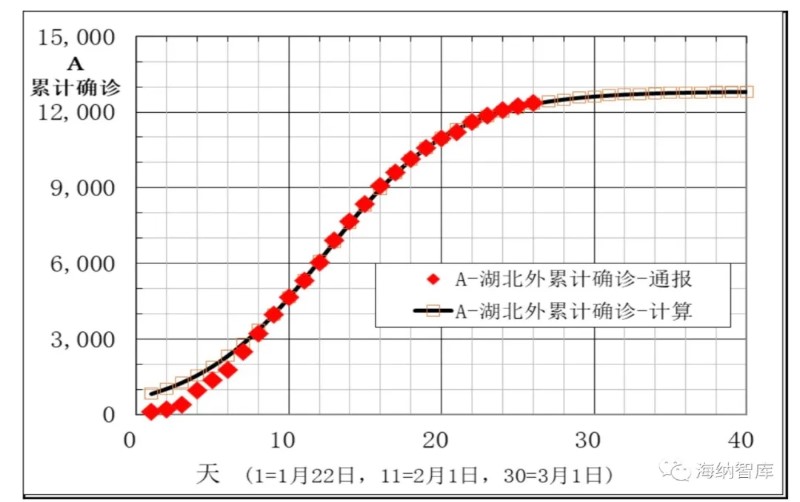
图1: 湖北外地区累计确诊数 A 通报和模型计算数据
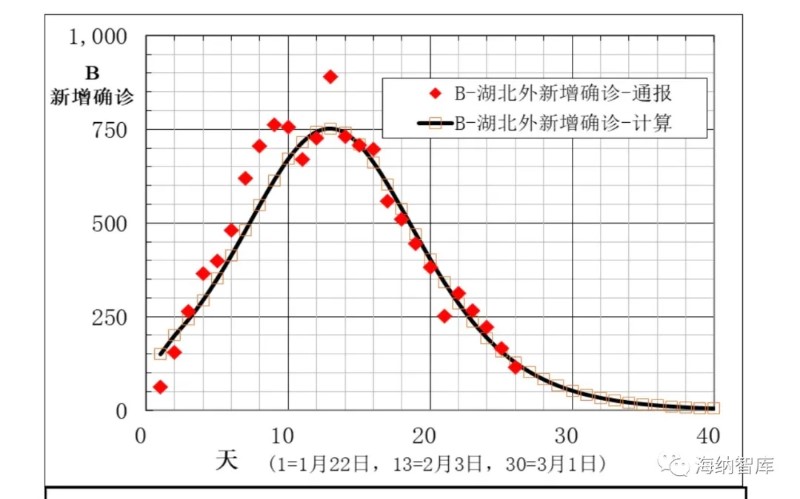
图2 湖北外地区每日新增确诊数B通报和模型计算数据(拐点区在2月2到4日)
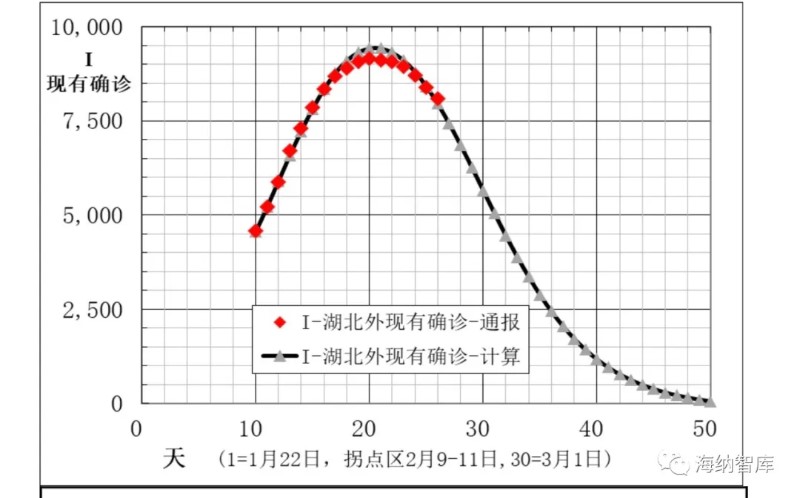
图3 湖北外地区现有确诊数I的通报和模型计算数据(拐点区在2月9到11日)
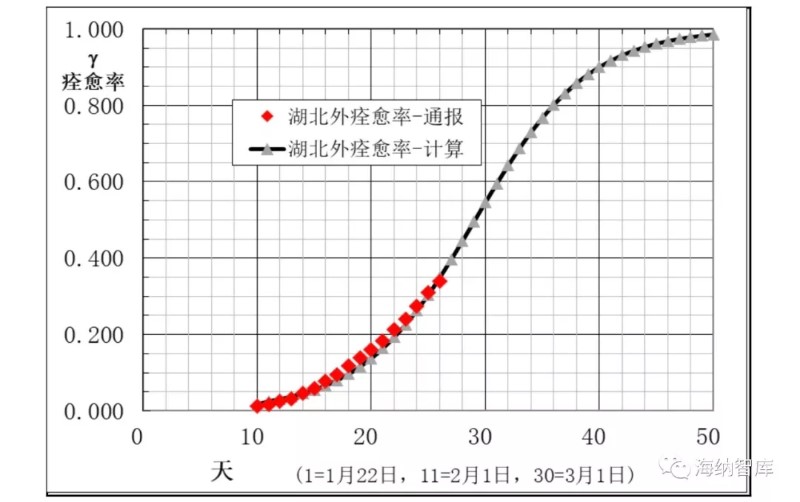
图4 湖北外地区痊愈率g通报和模型计算数据
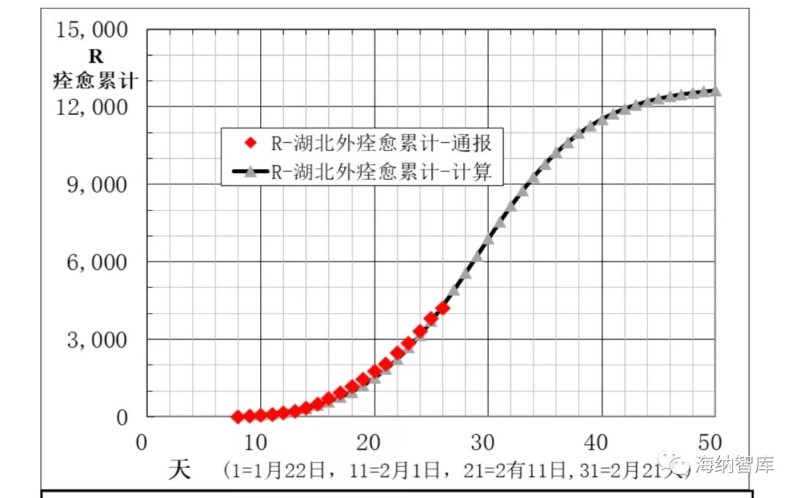
图5 湖北外地区累计痊愈数R通报和模型计算数据
湖北地区,病例通报和建模计算得到的主要数据,在下面图6-10中给出。从图6、7和8看出,2月5日到12日的8天,累计确诊数A,新增确诊数B,现有确诊数I的计算数据与通报数据偏差大,表明累计确诊通报数A不可靠。其他日期模型计算数与通报数符合较好。图9和图10中痊愈率和累计痊愈病例数R模型计算与通报数据相当一致,说明本文大胆提出的第二条假设,痊愈率也是逻辑回归函数非常合理。
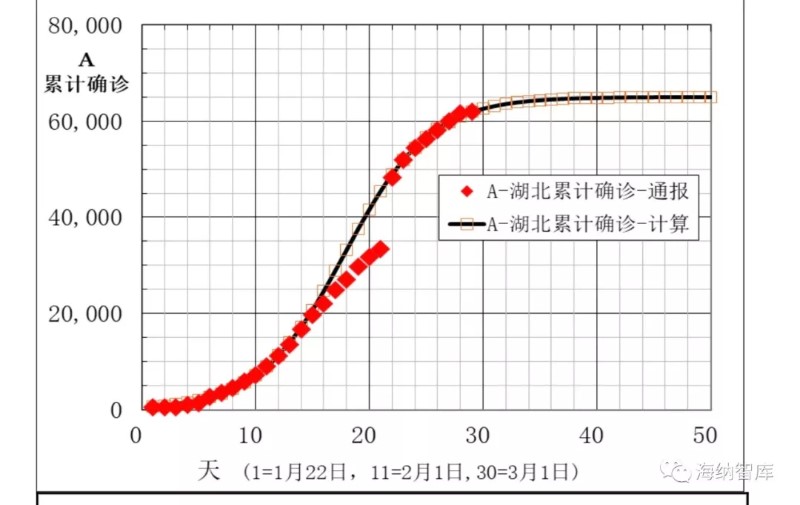
图6 湖北累计确诊数A通报和模型计算数据
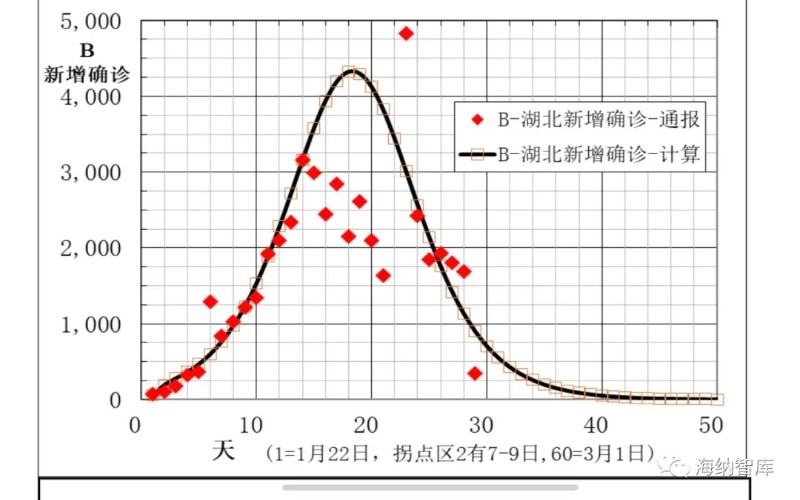
图7 湖北每日新增确诊数B通报和模型计算数据
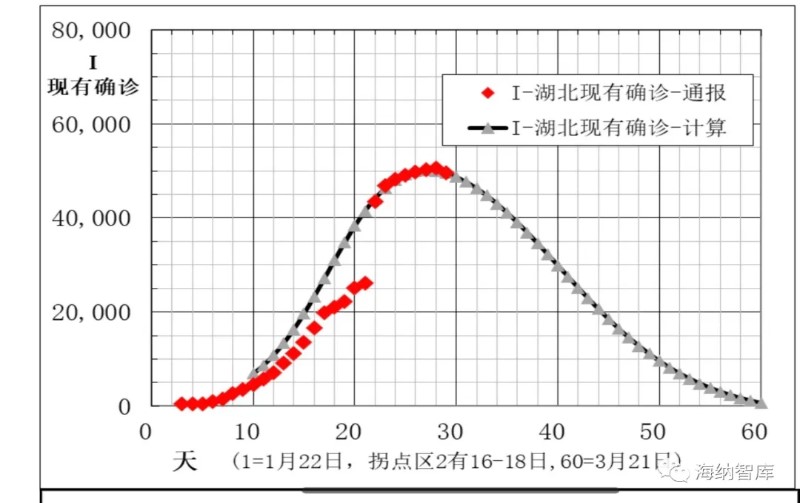
图8 湖北现有确诊数I通报和模型计算数据(预测拐点区2月16到18日)
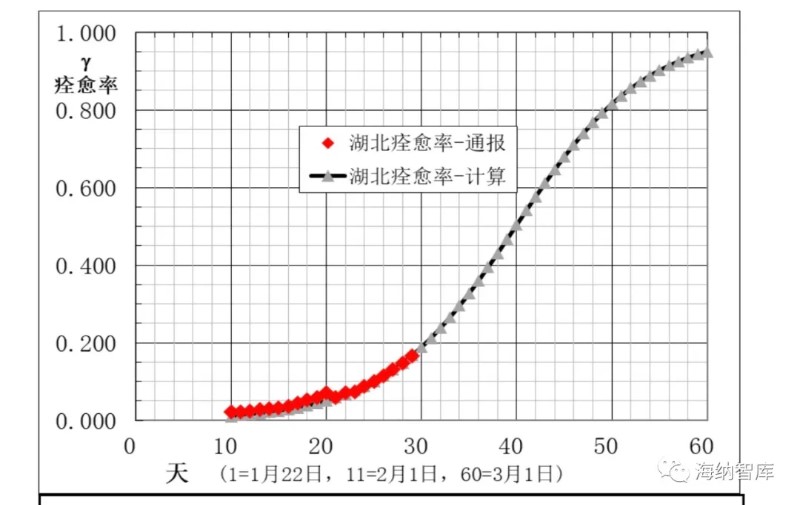
图9 湖北痊愈率g通报和模型计算数据
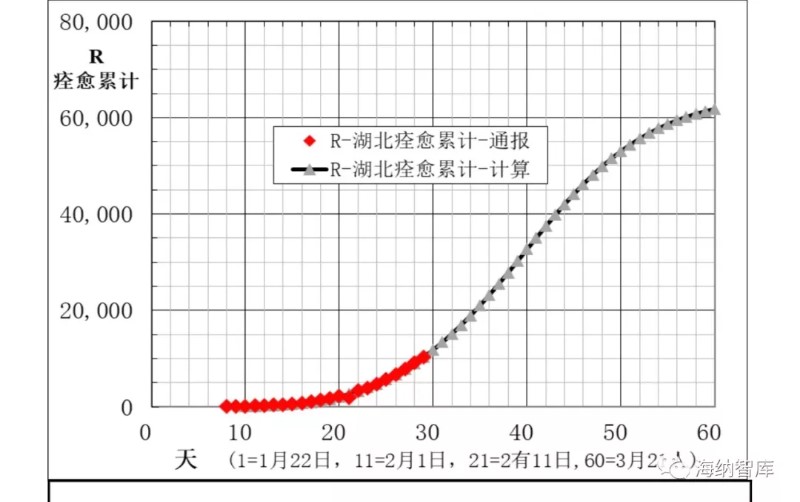
图10 湖北痊愈累计数R通报和模型计算数据
本文中COVID-19疫情的2月11日前的通报数据由天津陈革正高工汇总提供,并参考了斯坦福大学Michael Levitt教授发表在网上的这次疫情模型计算论文中疫情早期数据,这里一倂感谢。
后记
正文题外话作为后记。
这是一篇科学类文章,为了响应中国科技部的号召,论文写在COVID-19疫情过程中,因此作者决定在《海纳智库》及其网站上发表,提供给各类学者和网友,及相关政府部门参考。在网上发表时,把微分方程,逻辑回归函数表达式,复杂的计算过程略去。
传染病COVID-19从2019年12月开始出现,到今年1月下旬开始大规模爆发。本文作者关心疫情,从网上看了大量报道。其中仔细阅读了网上有关建模计算传染病COVID-19疫情报道,包括介绍Nature,Science, 柳叶刀等国际学术刊物预印本有关传染病COVID-19动力学建模计算综合报道,钟南山院士团队疫情预测报道,清华大学团队建模计算给出的疫情数据图等。特别是本文作者仔细阅读了在今日头条网站转载的斯坦福大学Michael Levitt教授在网上发表的COVID-19疫情模型计算学术性文章。
本文作者章其初博士,二十多年前在悉尼大学物理学院,从事聚光太阳能热发电有关的光热转换金属陶瓷材料和节能玻璃领域的物理实验研究期间,完成过两项复杂物理过程和大量实验数据建模计算,一项被专业学术刊物主编评价为“Excellent work”,另一项被国际同行评价为“Amazing”。
作者在上述建模计算过程中,积累了一些经验,因此想跨学科,试一试传染病动力学建模计算工作,用来分析和预测COVID-19流行病疫情。作者手头有关资料缺乏,只有在网上阅读了一些有关传染病动力学模型的一些文章,还没有阅读过在学术刊物上发表的传染病建模计算的论文。所以,若有人发现了类似的传染病模型论文,烦请告知发表本论文的网站,或《海纳智库》和作者本人。
Kermack与McKendrick在1927年提出的传染病SIR舱室模型至今已有近百年了,还没有重大突破。本文作者在已有各种模型中,提取有用部分,再提出一些新的构思和大胆但合理的假设,建立的传染病动力学SARD模型,迈出传染病动力学模型计算的一大步,从函数没有解析解到找到了解析解。
传染病学和其他专业学者,及网友,可以采用本SARD模型进一步深化研究,写出可以在Nature,Science,以及中国和国际医学类等学术刊物上发表的高质量论文。提醒大家,到时不要忘记感谢本文作者章其初,SARD模型提出者,以及发表的网站及《海纳智库》。发表本论文网站是志愿者编辑和维护的。另外,医学领域的学者模型数值计算有困难,作者可以协助计算,并提供计算得到的数据。
最后,希望政府相关机构,或网站,把这次传染病COVID-19疫情数据制作成表格式数据库,以便“大数据库挖矿的矿工们”下载运用。另外,希望阿里巴巴公司做一个【科学论文预印本】网站,免费提供给作者快速发表学术论文,为祖国科技发展做出另一类贡献。
